这是十年前的工作了,现在才来记录一下。
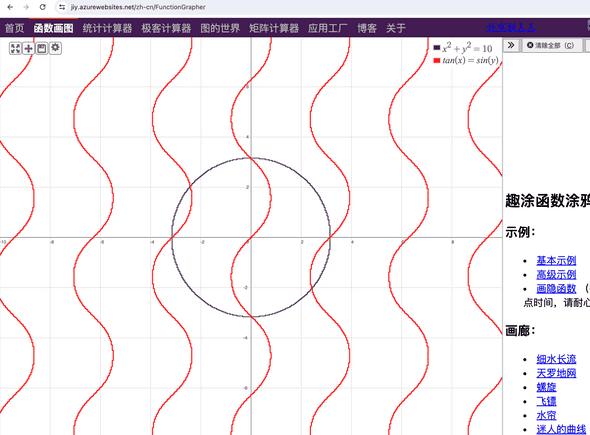
画显函数非常容易,但是画隐函数还是挺难的。十几年前,我基于 jQuery flot 插件,做了一个尝试。那个时候, https://www.desmos.com/calculator?lang=zh-CN 也还不能画隐函数,所以一度引起了一些关注。
不过 desmos 迭代很快,现在已经非常非常强大了,远非我这个十年前的老程序所能比的。
尽管如此,我还是想将曾经做的一些工作稍微整理一下,并对比一下论文里的图形和我这个在线绘制工具画出来的样子。
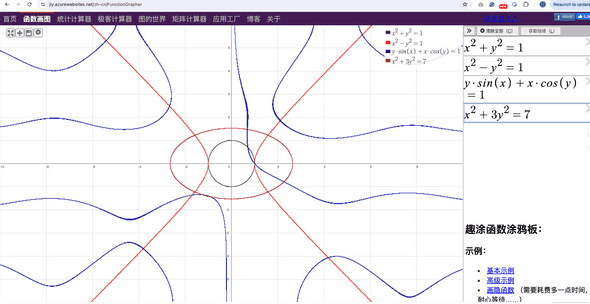
效果展示
https://jiy.azurewebsites.net/zh-cn/FunctionGrapher
源代码
https://github.com/pa-pa-me/zizhujy.com
原理
为了实现画隐函数,我参考了好几篇论文。借本篇博客,翻译其中一篇(同时纠正原文中的一些印刷错误),以方便更多人阅读,并节省自己将来再次阅读的时间。这篇论文是《绘制隐函数》,原文在此:http://homepages.warwick.ac.uk/staff/David.Tall/pdfs/dot1986b-implicit-fns.pdf
以下是我的翻译:
《绘制隐函数》的中文翻译
绘制隐函数
David Tall
<font style=color:rgb(13, 13, 13);>数学教育研究中心
<font style=color:rgb(13, 13, 13);>华威大学,考文垂 CV4 7AL
<font style=color:rgb(13, 13, 13);>一个常见的问题是将隐函数关系如椭圆:
$ x^2+2y^2+4x+6y=5 $
<font style=color:rgb(13, 13, 13);>转换为图形形式。通过代数运算,可以求解 $ y $<font style=color:rgb(13, 13, 13);> 的函数(使用正负平方根),然后在曲线上绘制点 $ (x,y) $<font style=color:rgb(13, 13, 13);>。但这种方法不易推广,对于更复杂的关系,如:
$ ysinx+xcosy=1 $
<font style=color:rgb(13, 13, 13);>几乎是不可能的。
<font style=color:rgb(13, 13, 13);>幸运的是,通过编程数值方法绘制更一般的隐函数
$ f(x,y)=常数 $
<font style=color:rgb(13, 13, 13);>可以不用显式求解关系。本文将通过 BBC BASIC 演示(这种语言能很好地表达数学结构),尽管这些技术可以翻译成其他具有用户定义函数和高分辨率图形的计算机。
<font style=color:rgb(13, 13, 13);>我们的方法可以理解为牛顿-拉弗森近似技术和偏导数的结合。但进行计算或理解理论并不需要微积分。这充分说明了可以在计算机上与微积分并行或甚至在其之前引入数值方法。我确信这将是学校数学教学的最终方向。因此,我将在不使用任何微积分的情况下撰写这篇文章。
<font style=color:rgb(13, 13, 13);>思路
<font style=color:rgb(13, 13, 13);>方程
$ f(x,y)=c $
<font style=color:rgb(13, 13, 13);>的解可以在更广泛的背景中理解。想象函数
$ z=f(x,y) $
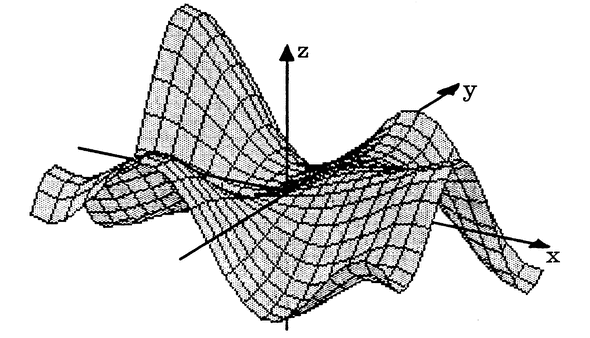
<font style=color:rgb(13, 13, 13);>的值在平面点 $ (x,y) $<font style=color:rgb(13, 13, 13);> 上方绘制高度为 $ z=f(x,y) $<font style=color:rgb(13, 13, 13);> 的点。结果是一个类似山脉的表面。例如,图 1 显示了
$ z=ysinx+xcosy $
<font style=color:rgb(13, 13, 13);>的图形,使用 Supergraph 包中的 “Super3D” 程序绘制(将 z 轴缩小三分之一以获得更好的图像)。
<font style=color:rgb(13, 13, 13);>发表于1986 年《Mathematics in School》第 15 章第 2 节(第 33-37 页)
<font style=color:rgb(13, 13, 13);>在表面上绘制的线是形式为 𝑥=常数 和 𝑦=常数 的线。
<font style=color:rgb(13, 13, 13);>隐关系
$ ysinx+xcosy=1 $
<font style=color:rgb(13, 13, 13);>由高度 𝑓(𝑥,𝑦)=1 的等高线上的所有点组成。我们可以通过计算
$ z=ysinx+xcosy $
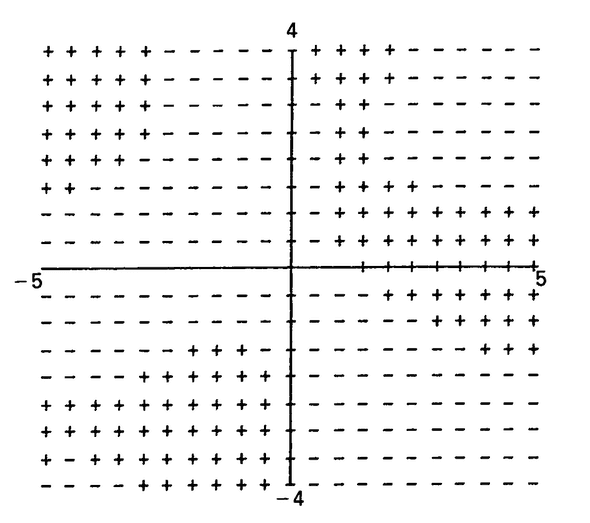
<font style=color:rgb(13, 13, 13);>在平面上某些点的值来大致了解等高线的位置,并标记这些点以区分满足 𝑧<1、𝑧=1 和 𝑧>1 的点。如果 𝑧=1 的点出现,这就给出了等高线上的一个点,如果没有,等高线将位于 𝑧>1 和 𝑧<1 的位置之间。图 2 在 𝑧<1 处标记 “-”,在 𝑧>1 处标记 “+”,标记间隔为 0.5。如果将此与原始表面进行比较,高度低于 𝑧=1 的山谷对应于 “-” 标记,高于 𝑧=1 的山峰对应于 “+” 标记。
<font style=color:rgb(13, 13, 13);>它们之间的等高线是满足隐关系 𝑦sin𝑥+𝑥cos𝑦=1 的点集。它由多个部分组成。要找到左上象限部分上的一个点,沿着 𝑦=2 的线查看,在 𝑥=−3.5 和 −3 之间存在符号变化。可以通过将 𝑦=2 代入原方程:
$ 2sinx+xcos2=1 $
<font style=color:rgb(13, 13, 13);>求解该方程以在 𝑥=−3.5 和 −3 之间找到一个根,我们将在接下来的两个部分中看到如何完成这一过程,然后再解决追踪等高线的主要问题。
图形的梯度
<font style=color:rgb(13, 13, 13);>图形上两点 (𝑎,𝑓(𝑎)) 、(𝑏,𝑓(𝑏)) 之间的梯度总是可以计算为
$ frac{f(b)-f(a)}{b-a} $
<font style=color:rgb(13, 13, 13);>但在曲线图上,这将取决于 𝑎 和 𝑏 的值。然而,如果图形的一个小段高度放大后看起来像一条直线,那么在该段中任意两个相邻点 (𝑎,𝑓(𝑎))、(𝑏,𝑓(𝑏)) 计算的梯度将大致相同。
<font style=color:rgb(13, 13, 13);>你可能不相信如圆形的曲线图可以近似直线。从某种意义上说,你是对的。但想象一下,你是一名专注的运动员(对我来说是个挑战,但希望对你不是)并且你正在绕着一条一公里长的环形跑道跑步。碰巧起雾了,所以你只能看到前方十米的距离。跑道在一公里内转了 360 度,也就是说在大约 27 米内转了一度;在有限的视野内,跑道看起来几乎是直的,尽管整体上它是一个完整的圆圈。
<font style=color:rgb(13, 13, 13);>同样地,在 A4 纸上绘制的圆 $ x^2+y^2=1 $<font style=color:rgb(13, 13, 13);> 显然是弯曲的,但如果将其中的一小部分以非常高的倍数放大,它将看起来几乎是直的。大多数以普通函数表示的图形在高度放大时具有这种“局部直线”特性。对于微分函数来说,这种特性是微积分的基础。我们的目的是在不使用微积分的情况下利用这种特性。
<font style=color:rgb(13, 13, 13);>要计算局部直线图形 𝑦=𝑓(𝑥) 上某点附近的梯度,我们取一个合适的小值,例如 𝑒=0.0001,并从 (𝑥,𝑓(𝑥)) 到 (𝑥+𝑒,𝑓(𝑥+𝑒)) 计算梯度。梯度大致为
$ frac{f(x+e)-f(x)}{e} $
<font style=color:rgb(13, 13, 13);>在计算机上,这可以分两步完成:首先以用户定义的形式表示函数,例如在 BASIC 中写为一行程序。比如,如果函数是 $ f(x)=x^2-2 $<font style=color:rgb(13, 13, 13);>,则写为
basic 10 DEF FNf(x) = x^2 - 2
<font style=color:rgb(13, 13, 13);>然后定义梯度函数 𝑔(𝑥) 为
basic 20 DEF FNg(x) = (f(x + e) - f(x)) / e
<font style=color:rgb(13, 13, 13);>使用该表达式之前需要输入一个 𝑒<font style=color:rgb(13, 13, 13);> 值,例如
basic LET e = 0.001
<font style=color:rgb(13, 13, 13);>然后输入以下内容以获得 𝑥=1 附近图形的(近似)梯度:
basic PRINT FNg(1)
<font style=color:rgb(13, 13, 13);>得到的值是 2.0010001。
<font style=color:rgb(13, 13, 13);>如果将 𝑒 改为 0.000567,则梯度为 2.0005663,与之前的值一致到 4 位有效数字。其他小值 𝑒 给出的梯度在 𝑥=1 附近大约等于 2。合理的 𝑒 值大约为 1E–4。更小的值会因为除以一个很小的数而导致精度丢失。以同样方式可以获得其他点附近的梯度。
<font style=color:rgb(13, 13, 13);>牛顿-拉弗森技术
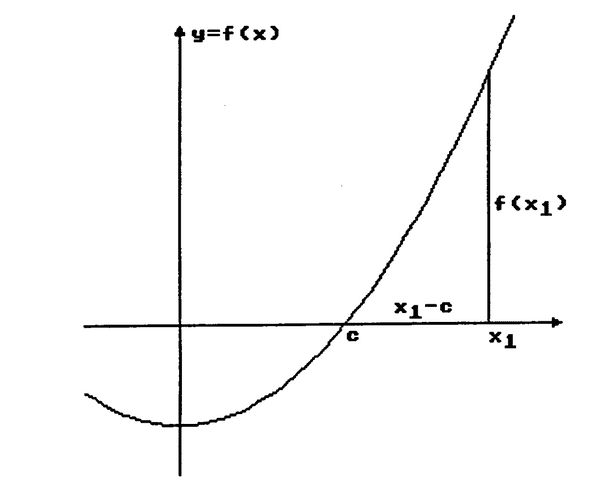
<font style=color:rgb(13, 13, 13);>假设 𝑦=𝑓(𝑥) 在 𝑥=𝑐 处与 x 轴相交,因此 𝑓(𝑐)=0,并且 𝑥1 足够接近 𝑐<font style=color:rgb(13, 13, 13);>,使得图形几乎是直线的。(图 3)
 <font style=color:rgb(13, 13, 13);>
<font style=color:rgb(13, 13, 13);>
<font style=color:rgb(13, 13, 13);>从点 (𝑐,0)(图形与 x 轴相交的点)到 (𝑥1,𝑓(𝑥1)) 的图形梯度为
$ frac{f(x_1)}{x_1-c} $
<font style=color:rgb(13, 13, 13);>但在 𝑥=𝑥1 处的图形梯度大致为
$ g(x_1)=frac{f(x_1+e)-f(x_1)}{e} $
<font style=color:rgb(13, 13, 13);>因此
$ frac{f(x_1)}{x_1-c}approx g(x_1) $
<font style=color:rgb(13, 13, 13);>并且
$ capprox x_1-frac{f(x_1)}{g(x_1)} $
<font style=color:rgb(13, 13, 13);>如果我们令
$ x_2=x_1-frac{f(x_1)}{g(x_1)} $
<font style=color:rgb(13, 13, 13);>那么 $ x_2 $<font style=color:rgb(13, 13, 13);> 可能是一个比 $ x_1 $<font style=color:rgb(13, 13, 13);> 更接近 𝑐<font style=color:rgb(13, 13, 13);> 的值。此过程可重复进行:
$ x_{n+1}=x_n-frac{f(x_n)}{g(x_n)} $
<font style=color:rgb(13, 13, 13);>得到越来越接近 𝑐 的值 $ x_n $<font style=color:rgb(13, 13, 13);>。这就是牛顿-拉弗森技术。
<font style=color:rgb(13, 13, 13);>在计算机程序里,我们可以去掉后缀并简单地说只要 x 是一个足够接近根的值,那么
$ x-f(x)/g(x) $
就通常会是一个更好的值。从而我们就能使用 $ x-f(x)/g(x) $来替换 x,并不断重复这个过程。
当$ f(x)=x^2-2 $时,我们可以使用下面的程序来不断打印方程$ c^2-2=0 $的根的接替近似值,直到结果精确到 1E-5 以内再停下来:
basic 5 p=0.001 10 DEF FNf(x)=x^2-2 20 DEF FNg(x)=(FNf(x+e)-FNf(x))/e 30 INPUT x= x 40 REPEAT 50 x = x-FNf(x)/FNg(x) 60 PRINT x 70 UNTIL FNf(x)<1E-5
如果计算机语言没有 REPEAT 指令,那就删除第 40 行,并将第 70 行替换成:
basic 70 IF FNf(x) > 1E-5 THEN 30
从 x=1 开始,BBC 计算机给出了如下的数列:
1.4999764
1.41666808
1.41421537
<font style=color:rgb(13, 13, 13);>误差容限1E–5还可以进一步减小:<font style=color:rgb(31, 31, 33);background-color:rgb(249, 249, 251);>在BBC计算机上e=1E–5可以在只多一次迭代的情况下得到√2=1.41421356,这是该机器的最大精度。在BBC计算机上我们可以用以下代码替换第10行:
basic 10 INPUT f(x) = f$ 15 DEF FNf(x)=EVALfS
<font style=color:rgb(31, 31, 33);background-color:rgb(249, 249, 251);>以便在程序运行时允许将函数作为BASIC字符串输入。这种技术将用于主程序。
<font style=color:rgb(13, 13, 13);>追踪轮廓线
在追踪隐函数 f(x,y)=c 的图形时,初始步骤是找到一个点作为开始绘图程序的起点。技术方法是估计一个接近曲线的点 (x,y),然后固定 x 或 y 中的一个,使用牛顿-拉弗森方法移动另一个点到曲线上。主要任务是追踪轮廓线。最近在Peak District徒步时,我发现山上经常有几条路径相互交叉。通常可以从某个高度开始,通过下行一条路径并转向另一条路径,然后上行,来到达同一高度的另一个地方。在之前使用Super3D绘制的三维图像中,表面 z=f(x,y) 被路径 x=常数 和 y=常数 所穿过。为了从某个高度的一个点移动到附近同一高度的另一个点,一个好的攻击计划是沿着表面的 x=常数 线条下行,然后转90度,沿着 y=常数 线条上行适当距离回到原来的高度。如果 x 变化而 y 保持不变,表面上 (x,y) 之上路径的梯度大约是
$ g_1(x,y)=(f(x+e,y)-f(x,y))/e $。
同样地,如果 y 变化而 x 保持不变,表面上 (x,y) 之上路径的梯度大约是
$ g_2(x,y)=(f(x,y+e)-f(x,y))/e $。
因此,从 (x,y) 到 (x+h,y) 的 x 步长 h 会导致 z 方向上升高
$ hg_1(x,y) $。
此时,保持 x+h 固定,并在 y 方向上取步长 k 到达 (x+h,y+k) 将进一步改变高度
$ kg_2(x+h,y) $。
因此,从 (x, y) 到 (x+h, y+k) 的总高度变化大约是
$ hg_1(x,y)+kg_2(x+h,y) $。
如果这时正好回到了出发前的高度,那就是说总高度变化正好是 0:
$ hg_1(x,y)+kg_2(x+h,y)=0 $。
这个方程允许我们以 h 为条件确定 k:
$ k=-frac{hg_1(x,y)}{g_2(x+h,y)} $
(前提是 $ g_2(x+h,y)neq0 $。)
然而,尝试以 k 为条件写出 h 会得到
$ h=-frac{kg_2(x+h,y)}{g_1(x,y)} $。
这在等式右边涉及到 h。如果 $ g_2(x+h,y) $ 和 $ g_2(x,y) $相当接近,那么解决这个难题的最简单方法是用 $ g_2(x,y) $ 替换 $ g_2(x+h,y) $,得到一个更简单(但可能更糟)的近似
$ hg_1(x,y)+kg_2(x,y)=0 $。
然后这个单一近似可以用来确定 h 以 k 为条件,或者 k 以 h 为条件,取决于哪个更合适。
为了保持 h 和 k 的适度大小,一个巧妙的技巧是指定一个步长,并取 k, h 中较大的一个为这个大小。首先让
$ H=g_2(x,y), K=g_1(x,y) $
这样
$ Hg_1(x,y)+Kg_2(x,y)=0 $。
如果 |H|>|K|(特别是意味着 H≠0),那么我们取 x 步长为大小 s。为了确保我们的方向与 H 相同,我们实际上取
$ h=scdot SGN(H) $,
然后令 $ k = hcdot frac{K}{H} $。
BASIC 中的完整规则(ii)是:
basic IF ABS(H)>ABS(K) THEN h=sSGN(H) : k=hK/H ELSE IF K<>O THEN k=sSGN(K) : h=kH/K
然后用 x+h 和 y+h 替换 x, y 的值,得到沿轮廓线进一步的一个新点。任何不准确性可以通过在下一步之前进一步使用牛顿-拉弗森技术来改进。
绘制隐函数的一个程序
我们现在终于可以来介绍主程序了。坐标轴使用 PROCdraw_axes绘制,然后在输入函数 f(x, y) (以 BASIC 字符串的形式)和常数 c 之后,使用过程 PROCplot_colour来绘制点数组 (x, y):
basic in red if f(x, y)<c, yellow if f(x, y)=0 and white if f(x, y)>c.
(如果你的显示器不能很好地区分黄色和白色的点,则添加如下行:
basic 2O15 VDU 19,3,6;O;
来将白色改成青色。)
主要的 REPEAT 循环让 x, y 的值成为输入,并且 y 的值会被不断改进以更接近需要的轮廓线。步长 s 是程序接下来用来跟踪隐函数的图形周边的。这个图形绘制会一直进行到 SHIFT 键被按下(INKEY(-1)),这时程序返回,允许移动画布到别处从而绘制另一部分的轮廓。要绘制反方向的轮廓,只需要改变步长的正负号就行了。
要完全停止这个程序,可以同时按下 CTRL 键(即最后的 INKEY(-2) 条件)和 SHIFT 键,或者按住 ESCAPE 键即可。
basic 1O MODE 1 2O PROCdraw_axes 6O INPUT f(x,y)= f$ 7O INPUT c= c 8O PROCplot_colour : REM plot array of coloured dots for +/- 9O REPEAT : CLS : REM - main program loop 1OO INPUT exact x= x 11O INPUT approx y= y 12O PROCimprove_y : REM get accurate y for given x 13O PRlNT exact y= ;y 14O PLOT 69,1OOx,1OOy : REM - plot start point 15O INPUT step s= s 16O REPEAT : REM - drawing loop for a solution curve 17O H=-FNg1(x,y):K=FNy2(x,y) 18O IF ABS(K)<ABS(H) THEN h=sSGNH:x=x+h:y=y+hK/H:PROCimprove_y ELSE IF K<>O THEN k=sSGNK:y=y+k:x=x+kH/K:PROCimprove_x 19O DRAW 1OOx,1OOy : REM - join to next point 2OO UNTIL INKEY(-1) : REM - until SHIFT key pressed 21O UNTlL INKEY(-2) : REM - until CTRL key pressed 22O END 1OOO DEF FNf(x,y)=EVALf$ 1O1O DEF FNg1(x,y)=(FNf(x+e,y)-FNf(x,y))/e 1O2O DEF FNg2(x,y)=(FNf(x,y+e)-FNf(x,y))/e 2OOO DEF PROCdraw_axes 2O1O VDU 29;64O;48O; : REM - set graph window size 2O2O VDU 24,O,3,39,O : REM - set text window size 2O2O DRAW -5OO,O : MOVE 5OO,O : REM - start to draw axes 2O3O DRAW O,-5OO : MOVE O,5OO 2O4O VDU 5 : MOVE -564,-4 : PRINT -5 2O5O MOVE 5OO,-4 : PRINT 5 : VDU4 2O6O ENDPROC 3OOO DEPROCplot_colour 3O1O FOR x=-5 TO 5 STEP 1/2 3O2O FOR y=-s TO s STEP 1/2 3O3O z = FNf(x,y) 3O4O IF z<c THEN GCOL O,1 ELSE IF z=c THEN GCOL O,2 ELSE GCOL O,3 :REM - set colour 3O5O PLOT 6,1OOx,1OOy : REM - plot point colour 3O6O IF INKEY(-1) THEN x=5 : y=5 :REM touch SHIFT to quit 3O7O NEXT 3O8O NEXT 3O9O GCOL O,2 : REM - reset colour 3O95 ENDPROC 4OOO DEF PROCimprove_y 4O1O IF FNg2(xy)=O THEN ENDPROC 4O2O REPEAT 4O3O y=y-(FNf(x,y)-c)/FNg2(x,y) 4O4O UNTIL ABS(FNf(x,y)-c)<1E-5 OR FNg2(x,y)=O OR INKEY(-1) 4O5O ENDPROC 5OOO DEF PROCimprove_x 5O1O IF FNg1(x,y)=O THEN ENDPROC 5O2O REPEAT 5O3O x=x-(FNf(x,y)-c)/FNg1(x,y) 5O4O UNTIL ABS(FNf(x,y)-c)<1E-5 OR FNg1(x,y)=O OR INKEY(-1) 5O5O ENDPROC
当程序运行起来后,输入函数:
$ f(x,y)=x^2+y^2 $,即 f(x,y)=x^2+y^2
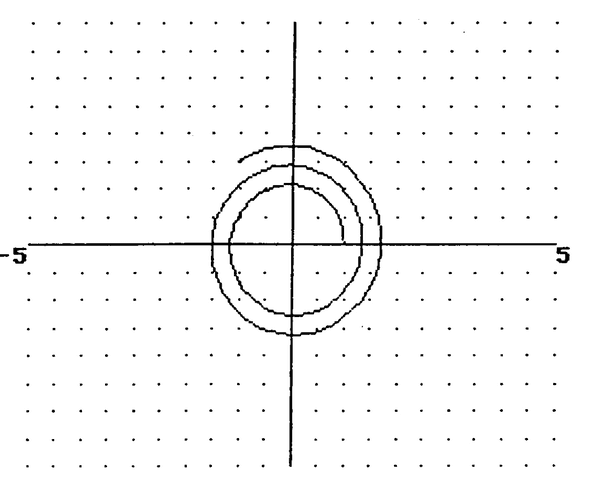
以及常数,并且从 (x,y) = (1, 0) 处开始,设置步长 s = 0.1。这个隐函数的曲线绘制其实就是单位圆:
$ x^2+y^2=1 $。
这个图片是令人满意的,因为在程序的第 180 行的牛顿—拉弗森近似值会将每个阶段的计算都拉回到曲线上。删除 PROCimprove_y和 PROCimprove_x就会导致程序中的绘制变得越来越差。比如当 s = 0.1 时,最后的结果会是一个螺旋向外的图形,如图 4 所示:
要画抛物线
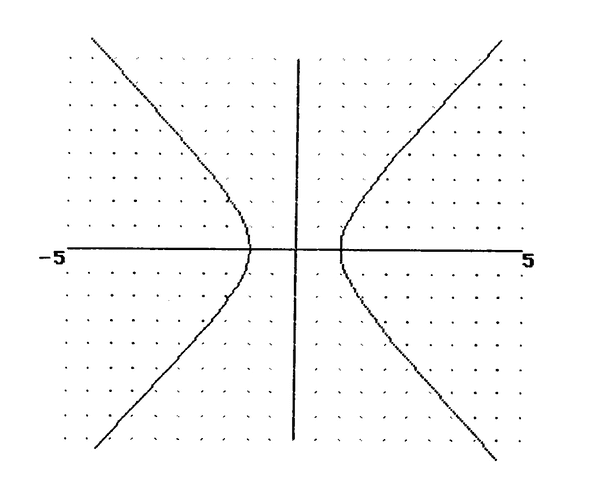
$ x^2-y^2=1 $,
从(1,0)开始,设置s=0.2,然后回到同样的点使用s=-0.2来绘制反方向上的曲线,再从(0, 1)重复这个过程从而得到另一个分支的曲线。(如图 5 所示。)
最难的图形
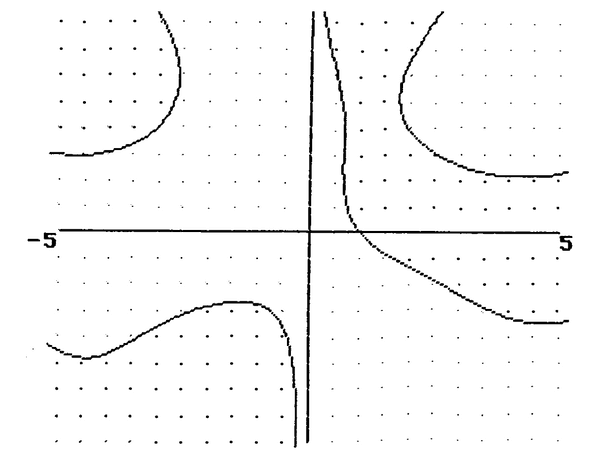
$ ysinx+xcosy=1 $。
可以多次使用这种技术来绘制(如图 6 所示。)
注意程序不仅绘制了方程 $ f(x,y)=c $。它还为区域 $ f(x,y)<c,f(x,y)>c $画上了阴影,所以它不仅表示了等式,还表示了不等式。
你可以用它来绘制另外的你想要画的隐函数,但是要知道绘制中的每一步都需要很多计算,所以复杂的表达式会画更长的时间来绘制。BBC BASIC 是这门语言中的快速版本,但在需要很多计算的情况下仍然不够快。
修正和改进
可以通过修改程序来获得更多关于它的工作机理的洞见,或者来改进它的服务。要获得洞见,一个思路可能是插入如下代码
basic 4OO5 count=O 4O25 count=count+l
以及插入同样的代码到 5005 和 5025 行,然后添加
basic 195 PRINT TAB(2O,13);count;
来检视需要多少额外的迭代来获得达到指定精度要求的隐函数的曲线。论文原作者的计算机上有Acorn 极速芯片,所有他添加了这一行
basic 195 SOUND-1,48+count*1OO
而不是前者(PRINT 那个),以收听<font style=color:rgb(31, 31, 33);background-color:rgb(249, 249, 251);>Kenneth Kendall那悦耳的嗓音报出号码(1986年的Acorn计算机内置了一个语音芯片,其中包含了BBC新闻播报员Kenneth Kendall所发音的一个小型词典。这个词典包括数字名称,并且可以通过SOUND命令来调用。)。
<font style=color:rgb(31, 31, 33);background-color:rgb(249, 249, 251);>同步并不完美,但它增添了一定的文化品质。这表明牛顿-拉弗森近似法只需要非常少的迭代次数就能达到所需的精度,在紧急转角处可能需要多走一两步。
<font style=color:rgb(31, 31, 33);background-color:rgb(249, 249, 251);>一个改进方法可能是在plot_colour过程中用线段替换点,线段的方向沿着曲线,使用以下额外的代码行:
basic 3O52 H=-FNg2(x,y):K=FNg1(xy) 3O54 1F H=O THEN a=O : b=12 ELSE G=K/H : a=12/SQR(1+G^2) : b=a*G 3O56 PLOT O,-a,-b : PLOT 1,a+a,b+b
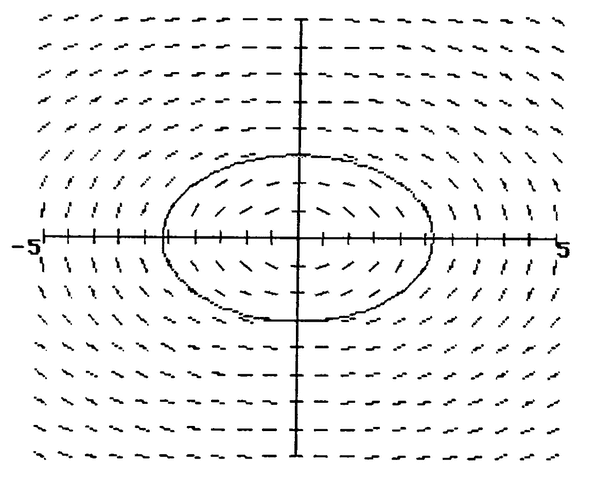
图 7 显示了用这种技术绘制的椭圆
$ x^2+3y^2=7 $
,并用其他椭圆
$ x^2+3y^2=常数 $
展示了方向线条。
实验机会在你手上,这正是修改给定程序的漂亮之处。这个思路强大的地方在于提供了实用的数学实践。数值程序方法以及这个方法的绘制结果应该在不远的将来成为数学课程中的一部分。
挑战
你能修改程序从而一旦输入了函数就不需要任何用户的打断,就自动绘制隐函数的图像吗?(尽管不够快,但应该精确……)(一个实现这个功能的程序被整合在Supergraph一系列程序中。它可以在不到一分钟的时间内绘制出一个隐函数。后来,当Archimedes计算机引入了快速的RISC芯片时,同样的程序只需要两到三秒钟就能操作完成。)
<font style=color:rgb(13, 13, 13);>此方法可以适用于各种函数关系,无需显式解或微积分,是一个强有力的工具。
<font style=color:rgb(13, 13, 13);>参考文献
l. Tall, David (1985) SuperGraph, textbook and disc of interactive graph drawing programs for the BBC computer, Glentop Publishing, D.V.