当你面对多条信息做决策时,可以从信息量最大的那条开始。
从排序开始
这一原则,适用于排序逻辑。举个例子,甲乙丙丁赛跑,给你以下 3 条信息,让你推断其完赛顺序:
- 有一个人排在乙和丙中间
- 有两个人排在丙和丁中间
- 乙不是第二名
请问,他们的名次是怎样的?谁是第一、谁是第二、谁是第三、谁是第四?
| 第一名 | 第二名 | 第三名 | 第四名 |
|---|---|---|---|
| ? | ? | ? | ? |
| 甲 | 乙 | 丙 | 丁 |
由于一共只有 4 个名次,以上 3 条信息中,第二条信息含量最大。我们可以知道,丙和丁中间必定有一个人是第一名,另一个是第四名。我们可以先假设丁是第一名,那么丙就是第四名:
| 第一名 | 第二名 | 第三名 | 第四名 |
|---|---|---|---|
| 丁 | 丙 | ||
| 甲 | 乙 |
接着我们看第一条信息,乙和丙中间有一名选手。由于我们假设了丙在第四名,乙就只能是第二名。这和第三条矛盾,所以我们之前的假设是错误的。于是得知丁必定是第四名,而丙是第一名:
| 第一名 | 第二名 | 第三名 | 第四名 |
|---|---|---|---|
| 丙 | 丁 | ||
| 甲 | 乙 |
再看第一条信息,乙和丙中间有一名选手,所以乙是第三名。而一旦将乙放在第三名,那么甲就是第二名。这同时满足了所有的条件:
| 第一名 | 第二名 | 第三名 | 第四名 |
|---|---|---|---|
| 丙 | 甲 | 乙 | 丁 |
通过从信息量最大的条件开始,我们能够以最少的步骤推断出结果。
信息量的量化
以上是一个简单的例子,很容易看出第二个条件的信息量最大。如果希望将选择信息量最大的条件自动化,就需要一种量化信息量的方式。常用的对信息量的度量是信息熵,用它来刻画任意样例集的纯度。给定包含关于某个目标概念的正反样例的样例集 S,那么 S 相对这个布尔型分类的熵为:
Entropy(S) = -p+log2(p+) - p-log2(p-)
其中,p+是在 S 中正例的比例,p-是在 S 中反例的比例。在有关熵的所有计算中我们定义 0log20 为 0。
亿点点解释
现在来解释一下为什么要这样来计算信息量,在构建决策树时,它是指导该怎样做分叉的基础。假设现在碰到一个树的结点,它包括一系列的正例与反例。在仔细检查计算信息量的公式之前,先考虑一下我们对信息量指标的需求。
- 如果正例或者反例的数量为零,那么信息量指标也为零。
- 如果正例和反例的数量一样多,那么信息量指标为最大。
当然,以上要求对多个类别也成立,不仅仅只对两个类别。也就是说,如果一个结点中只包含一个类别,那么信息量指标为零,而如果包含多个类别,且它们的数量相等,这个信息量指标达到最大值。注意,这个信息量的数量指标,和信息含量是相反的。即信息含量越高,其指标值越小。而这个指标越大,表示越没有信息量。
这个指标就叫熵,我们所说的宇宙的热寂,就是熵达到最大值,即物质的分布达到了一个处处平均的状态,也就是没有信息量的状态,处处都一样嘛。在没有外部能量输入下的封闭系统总是会趋于这一状态,而要减熵就需要输入外部能量。
启发:对于如今这个自媒体时代,想要赚到钱,就需要提供有信息量的内容,人们只会为减熵付费(尽管有信息量的内容不一定是“好”的内容)。
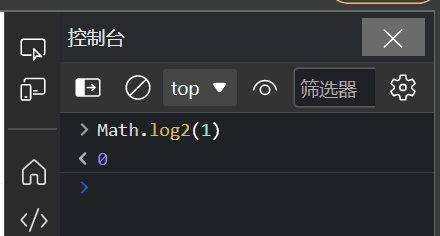
再回头看一下前面用来计算熵的公式,它正好满足我们的两点需求。当一个集合中只包含一个类别时,信息量最大,即熵为零,因为这时候这唯一的类别在集合中的比率为 100%, 也就是1,而 1 的对数为 0。
如果你在用网页的话,可以 F12 打开开发者工具,输入 Math.log2(1),即可验证:
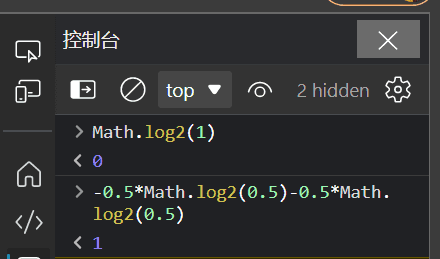
当一个集合包含的类别数量相等,比如正例和反例各占一半,即 50%。那么这时候熵就达到了包含两个类别的集合的最大值:1。
可以输入 -0.5Math.log2(0.5)-0.5Math.log2(0.5) 验证:
其他情况下,熵值在0到1之间。
熵的计算公式的特性
要满足我们对信息量的指标的那两点需求,有趣的是,似乎只有一个函数可以做到,这就是前面所展示出来的熵。前面展示的公式是一个包含着两个类别实例的集合的特例,对于包含 n 个实例的集合,其熵的计算公式如下:
Entropy(p1, p2, ..., pn) = -p1log2(p1) - p2log2(p2) - ... - pnlog2(pn)
之所以用负号,是因为比率值都是小于1的,而小于1的数,其对数是负数。为了让熵值为正,所以在公式中用了负号。正如公式所表明的,对比率取对数时,使用的底是 2。而熵的单位,也叫做比特,就和计算机中的比特名字一样。
公式中的参数 p1, p2, ..., pn,不仅可以用小数,也可以用分数表示。总之,它们的和为 1。
熵的计算公式满足如下特性,这在多阶段决策时非常有用:
Entropy(p, q, r) = Entropy(p, q+r) + (q+r) x Entropy(q/(q+r), r/(q+r))
其中 p+q+r=1。
当比率用分数表示,再结合对数函数的特性,可以在实际的计算中,不必真正计算小数。举个例子,一个集合,包含3种类别的实例,第一种类别有2个,第二种有3个,第三种有4个,那么:
Entropy(2, 3, 4) = -2/9 x log(2/9) - 3/9 x log(3/9) - 4/9 x log(4/9)
= [-2 x (log2 - log9) - 3 x (log3 - log9) - 4 x (log4 -log9) ] / 9
= (-2log2 - 3log3 - 4log4 + 9log9) / 9
= 1.5304930567574824 比特
用熵来辅助构建决策树 —— ID3 算法
要构建一棵决策树,可以递归地实现。首先,选择一个属性放在根结点,然后针对该属性的每一个取值,都拉出一个分支。这就将一个大集合拆分成了多个子集,每个子集都对应所选属性的一个取值。将该过程对每个分支都重复地递归进行,一旦某个结点的所有实例都是同一类别,该结点就成为了叶子结点,不再对它进行拆分。
以上方法存在的唯一一个问题就是,每次拿到一个数据结点,该选择哪个属性来对其进行拆分呢?和最开始的排序示例一样,当然是选择信息量最大的那个属性。这就是 ID3 算法的基本思想。
考虑如下数据集(机器学习中著名的天气数据):
| # 属性 | <font style=color:rgb(0, 24, 70);>天气 | <font style=color:rgb(0, 24, 70);>温度 | <font style=color:rgb(0, 24, 70);>湿度 | <font style=color:rgb(0, 24, 70);>风 | <font style=color:rgb(0, 24, 70);>玩乐 |
|---|---|---|---|---|---|
| 1 | <font style=color:rgb(18, 6, 73);>晴朗 | <font style=color:rgb(18, 6, 73);>炎热 | <font style=color:rgb(18, 6, 73);>无 | <font style=color:rgb(18, 6, 73);>否 | <font style=color:rgb(18, 6, 73);>否 |
| 2 | <font style=color:rgb(18, 6, 73);>晴朗 | <font style=color:rgb(18, 6, 73);>炎热 | <font style=color:rgb(18, 6, 73);>高 | <font style=color:rgb(18, 6, 73);>无 | <font style=color:rgb(18, 6, 73);>否 |
| 3 | <font style=color:rgb(18, 6, 73);>多云 | <font style=color:rgb(18, 6, 73);>炎热 | <font style=color:rgb(18, 6, 73);>高 | <font style=color:rgb(18, 6, 73);>无 | <font style=color:rgb(18, 6, 73);>是 |
| 4 | <font style=color:rgb(18, 6, 73);>有雨 | <font style=color:rgb(18, 6, 73);>温暖 | <font style=color:rgb(18, 6, 73);>高 | <font style=color:rgb(18, 6, 73);>无 | <font style=color:rgb(18, 6, 73);>是 |
| 5 | <font style=color:rgb(18, 6, 73);>有雨 | <font style=color:rgb(18, 6, 73);>凉爽 | <font style=color:rgb(18, 6, 73);>中 | <font style=color:rgb(18, 6, 73);>无 | <font style=color:rgb(18, 6, 73);>是 |
| 6 | <font style=color:rgb(18, 6, 73);>有雨 | <font style=color:rgb(18, 6, 73);>凉爽 | <font style=color:rgb(18, 6, 73);>中 | <font style=color:rgb(18, 6, 73);>有 | <font style=color:rgb(18, 6, 73);>否 |
| 7 | <font style=color:rgb(18, 6, 73);>多云 | <font style=color:rgb(18, 6, 73);>凉爽 | <font style=color:rgb(18, 6, 73);>中 | <font style=color:rgb(18, 6, 73);>有 | <font style=color:rgb(18, 6, 73);>是 |
| 8 | <font style=color:rgb(18, 6, 73);>晴朗 | <font style=color:rgb(18, 6, 73);>温暖 | <font style=color:rgb(18, 6, 73);>高 | <font style=color:rgb(18, 6, 73);>无 | <font style=color:rgb(18, 6, 73);>否 |
| 9 | <font style=color:rgb(18, 6, 73);>晴朗 | <font style=color:rgb(18, 6, 73);>凉爽 | <font style=color:rgb(18, 6, 73);>中 | <font style=color:rgb(18, 6, 73);>无 | <font style=color:rgb(18, 6, 73);>是 |
| 10 | <font style=color:rgb(18, 6, 73);>有雨 | <font style=color:rgb(18, 6, 73);>温暖 | <font style=color:rgb(18, 6, 73);>中 | <font style=color:rgb(18, 6, 73);>无 | <font style=color:rgb(18, 6, 73);>是 |
| 11 | <font style=color:rgb(18, 6, 73);>晴朗 | <font style=color:rgb(18, 6, 73);>温暖 | <font style=color:rgb(18, 6, 73);>中 | <font style=color:rgb(18, 6, 73);>有 | <font style=color:rgb(18, 6, 73);>是 |
| 12 | <font style=color:rgb(18, 6, 73);>多云 | <font style=color:rgb(18, 6, 73);>温暖 | <font style=color:rgb(18, 6, 73);>高 | <font style=color:rgb(18, 6, 73);>有 | <font style=color:rgb(18, 6, 73);>是 |
| 13 | <font style=color:rgb(18, 6, 73);>多云 | <font style=color:rgb(18, 6, 73);>炎热 | <font style=color:rgb(18, 6, 73);>中 | <font style=color:rgb(18, 6, 73);>无 | <font style=color:rgb(18, 6, 73);>否 |
| 14 | <font style=color:rgb(18, 6, 73);>有雨 | <font style=color:rgb(18, 6, 73);>温暖 | <font style=color:rgb(18, 6, 73);>中 | <font style=color:rgb(18, 6, 73);>有 | <font style=color:rgb(18, 6, 73);>否 |
<font style=color:rgb(0, 24, 70);>决定是否玩乐的属性有 4 个,要将整个数据集做个拆分,拿哪一个来拆分比较好呢?
<font style=color:rgb(0, 24, 70);>如果用天气,得到的结果是:
如果用温度,得到的是:
如果用湿度,得到的是
如果用风这个属性,那么得到的是这样的子树:
哪个是最好的选择呢?在上面的子树中,是和否都列在了叶子结点里。只要哪个叶子结点只包含一个类别——全是或者全否——就不需要再进一步拆分了,递归进行到这个分支时就可以停下来。因为我们希望构建出来的树越小越好,所以希望这种全是或者全否的情况越多越好。
如果我们有一种办法来衡量每个结点的纯度,那么在每次选择属性时,去挑那种能够产生出最纯的子结点的属性就好了。从直观上看上面的 4 个子树图,只有选择天气这一属性时产生了一个全是的子结点,其他的都没有。
信息增益
当属性较多时,肉眼去看,是比较麻烦的。如果能够计算纯度,那就能够将挑选属性的过程自动化了。这个纯度,其实就可以用熵来计算。越纯,信息量越大,熵值越小。前面也介绍过了,其单位是比特。对照上面的树的结点来说,纯度对应了要将一个新的类别实例被归类为是或者否时所需要的信息数量。与计算机内存中的比特不同,所需要的信息数量比特一般都是小于1的!利用前面介绍的信息量(熵)计算公式,我们来计算一下以上4种情况下的信息量。
对于以上采用天气分拆的第一棵树,其子树中是和否的数量分别为:【2,3】、【4,0】以及【3,2】,这些结点的信息量分别为:
info([2, 3]) = 0.971 比特
info([4, 0]) = 0.0 比特
info([3, 2]) = 0.971 比特
我们将其平均,并考虑到每个分支中的实例数量:第一个分支、第三个分支都包含了5个实例,而中间的第二个分支包含了4个实例,以及去掉了。
info([2, 3], [4, 0], [3, 2]) = (5/14) x 0.971 + (4/14) x 0 + (5/14) x 0.971 = 0.693 比特
也就是说,使用第一个子树来对碰到的新实例进行归类的话,我们需要 0.693 比特的信息。
又,对于整个数据集来说,其包含了9个是,5个否。其信息量(熵)为:
info([9, 5]) = 0.940 比特
于是,第一个子树产生的信息增益是:
gain(天气)= info([9, 5]) - info([2, 3], [4, 0], [3, 2]) = 0.940 - 0.693 = 0.247 比特
这可以解释为使用天气来创建分支带来的信息量。采用这种方法,我们分别计算每一棵树的信息增益:
- gain(天气) = 0.247 比特
- gain(温度) = 0.029 比特
- gain(湿度) = 0.152 比特
- gain(风) = 0.048 比特
所以,我们选择天气做为第一次分支的属性,做为整棵树的根结点,这和我们前面用肉眼观察的结果一致。
我们递归地继续这个过程,进一步分拆,最终得到的结果(当一个结点不能再拆分或者进一步拆分得到的类别分布不变即信息增益是0时,就停下来)是:
优化
用分而治之(自顶向下的)的方法来构建决策树,是由悉尼大学的 J. Ross Quinlan 发明出来的,并经过了多年的迭代,并被称为 ID3。后来又有很多优化方案,比如 C4.5。
彩蛋
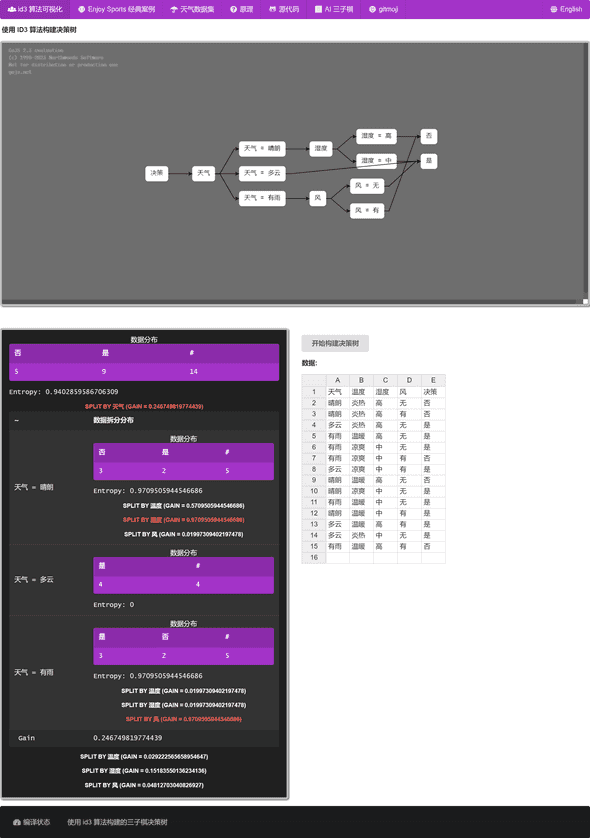
好多年前,做了一个在线展示 ID3 算法的可视化,详见: https://id3.js.org/?weather
另外,还做了一版 PPT 对 ID3 进行介绍,详见: